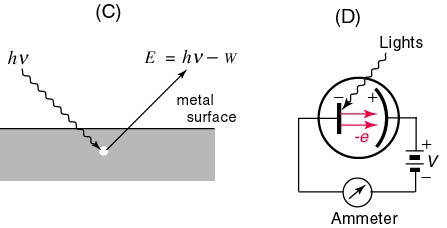
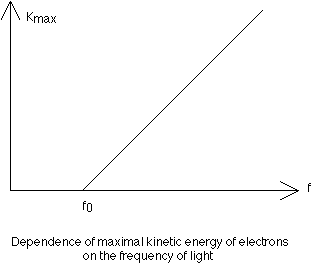The Photoelectric Effect. Light exerts a fascinating effect on certain metals such as zinc when they are charged negatively by contact. If these metals are exposed to various frequencies of incident light rays, it is determined that light in the ultraviolet range causes them to expel electrons. This rather interesting phenomenon does not occur if the metal is positively charged, however. This phenomenon is known as the photoelectric effect and it permits a new view of light that has come to be known as the quantum theory. The quantum theory, since its inception and development by Einstein in the early part of the 20th century, has been extended to particles as well as electromagnetic waves and constitutes the basis of modern physics. When a photoemissive material is exposed to light of a particular frequency, the emitted electrons are only sensitive to the intensity of the electromagnetic wave applied. The minimum frequency that results in the emission of electrons is termed the threshold frequency, fo. The energy of the emitted electrons is measured as the motion of the electrons is ceased as they approach a plate that is negatively charged in response to a source of potential difference (see figure). This is referred to as the stopping voltage or the stopping potential, Vo. The energy of the electrons stopped by this voltage is equal to the product of the electrons' charge and the stopping voltage eVo. Since the stopping voltage is independent
of the intensity of light, the stopping voltage measures the maximum kinetic energy of the emitted electrons. As the frequency of light is slowly increased, there is a change in the maximum kinetic energy of the electrons. The fact that this energy is independent of the intensity of the light was utilized by Einstein to demonstrate that light consists of discrete or quantized packets of energy called photons. The energy of a given photon is directly proportional to its frequency. The constant of proportionality relating KEmax of the electrons and the frequency of the source is the slope of the KEmax vs Frequency graph and is known as Planck's Constant (h = 6.63 x 10exp-34 J-s):
Slope = KEmax/(f - fo) = h.
This equation can in turn be used to solve for KEmax:
KEmax = hf - hfo.
This expression is known as the photoelectric equation, where hf represents the energy of the original photon, while hfo is the work function (a property of the metal) and is the minimum amount of energy required to expel an electron. Einstein's suggestion of the photoelectric effect was in direct conflict with the prevailing wave theory of light, as demonstrated by interference and diffraction, and therefore early 20th century physicists were presented with a dual nature of light. In the wave theory of light, the intensity of the light is related to its amplitude and is measured with a photometer. The intensity of the light energy varies inversely as the square of the distance from the source. In the quantum theory however, light intensity is related to the number, N, of photons:
N = Detected Energy/Energy of a Photon
In the photoelectric effect, when the intensity of the source is changed, only the number of photons, not their kinetic energy, is changed.
1. Light with a frequency of 2 x 10exp15 Hz is incident upon a sheet of copper. (a) Calculate the energy of the incident light in joules and in electron volts, and (b) calculate KEmax (in eV) of the emitted electrons given that the work function for copper is 4.5 eV.